
In January, OpenAI released two new embedding models: text-embedding-3-small and text-embedding-3-large. These models are trained with the Matryoshka Representation Learning technique, which lets developers trade off performance and cost in embeddings.
Since then, we’ve discussed Matryoshka embeddings in various formats, such as in our 89th Weaviate podcast episode, Matryoshka Embeddings with Aditya Kusupati, Zach Nussbaum, and Zain Hasan, and in our Weaviate paper review, Matryoshka Representation Learning.
This article briefly covers the fundamentals of Matryoshka Representation Learning and shows how to use the newly released OpenAI’s Matryoshka embedding models with the Weaviate vector database.
What is Matryoshka Representation Learning?
Matryoshka Representation Learning is a technique used in training embedding models. It allows you to trade off a small amount of accuracy in exchange for much smaller embedding sizes. Thus, you can store more information at a lower cost and search for it faster.
The embeddings are shortened by removing dimensions from the end of the sequence and only using a subset of the dimensions of the embedding vector. For example, you can only use the first 8, 16, 32, etc. dimensions (or any other slice of dimensions) of a vector that originally had 1536 dimensions.
In contrast to common vector embeddings, where all dimensions are equally important, in Matryoshka embeddings, earlier dimensions store more information than dimensions later on in the vector, which simply adds more details. You can think of this by the analogy of trying to classify an image at multiple resolutions: The lower resolutions give more high-level information, while the higher resolutions add more details.
Thus, the retrieval performance increases with increasing representation size. However, OpenAI reported that a text-embedding-3-large embedding can be shortened to a size of 256 while still outperforming an unshortened text-embedding-ada-002 embedding with a size of 1536 on the MTEB benchmark.
Retrieval performance over representation size for Matryoshka embeddings. (This image is based on Figure 7 in the original Matryoshka Representation Learning paper.)
The magic behind how MRL is carried out is all in the loss function which is optimized when training these models! If previously the loss function was L, for MRL we break down the loss function into the sum of the losses on individual vector dimension ranges: Loss_Total = L(upto 8d) + L(upto 16d) + L(upto 32d) + ... + L(upto 2048d). With this new nested loss function there is an incentive for the model to capture information in each sub-section of the vector.
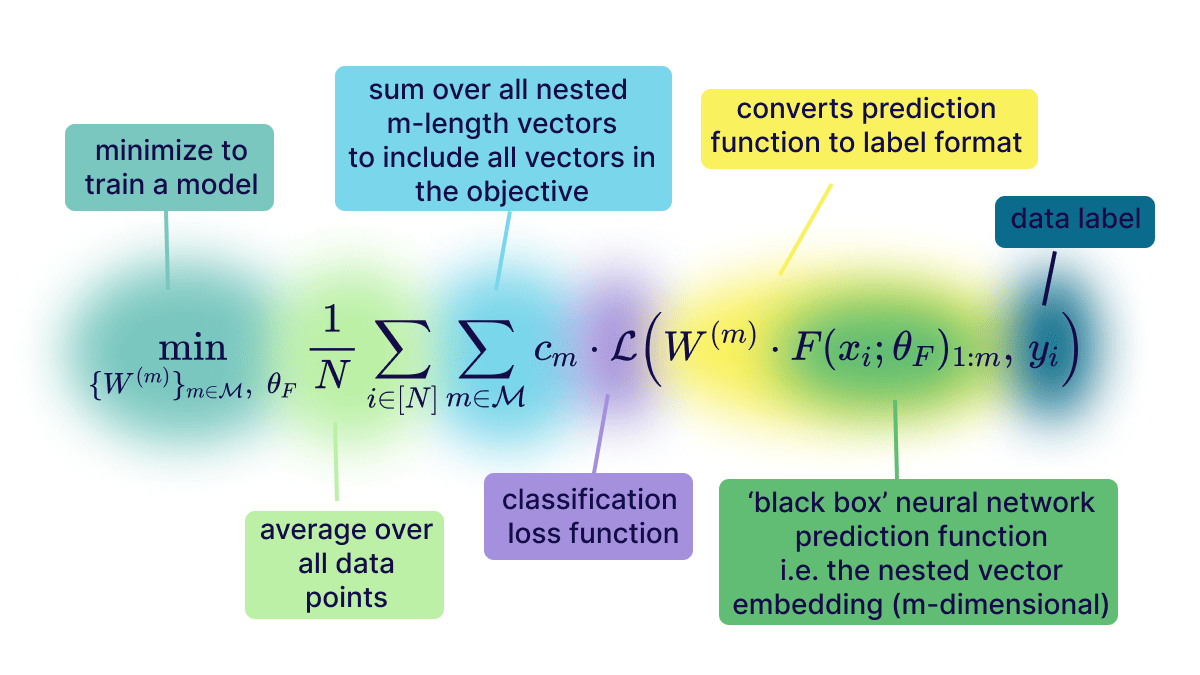
After modifying the loss you get these truncatable vectors for free wihtout any additional costs - this works on almost all loss functions and pre-existing models can be finetuned to output MRL vectors! This means that MRL is very easy to adopt and apply to pretrained models.
Detailed Analysis of Matryoshka Embeddings
Below we will work with a dataset of 1 Million objects from DBpedia that have been embedded using both the new OpenAI matryoshka text-embedding-3-large model aswell as the old ada-002 model. This will give us an understanding of how information is disproportionately stored in the the matryoshka vectors compared to thier non-matryoshka predecessors.
In this analysis below we sampled 10k random vectors from the dataset above and plotted out the standard deviation of values seen for each dimension. The variance or standard deviation seen across a dimension is a good proxy to measure how much information that dimensions carries relative to other dimensions.
| Matryoshka Vectors | Non-Matryoshka Vectors |
|---|---|
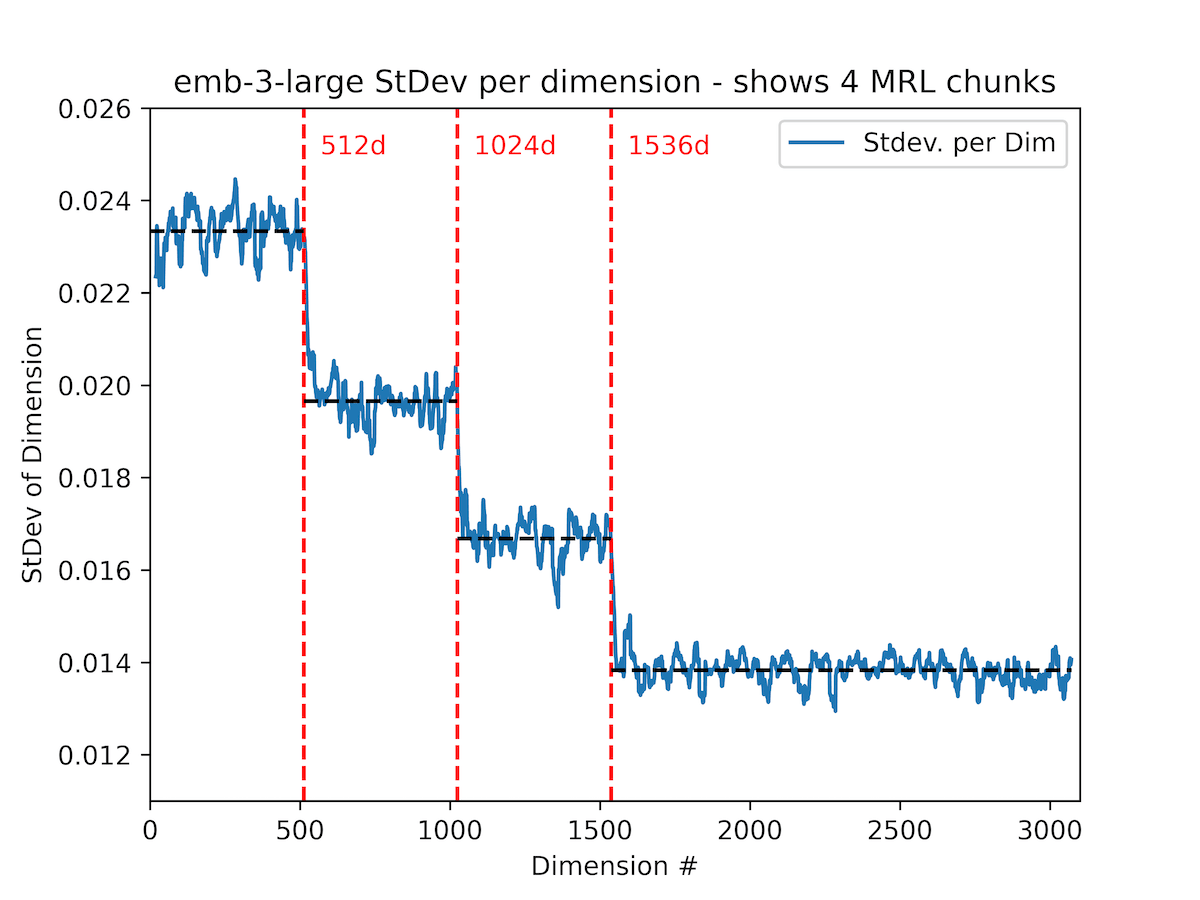 | 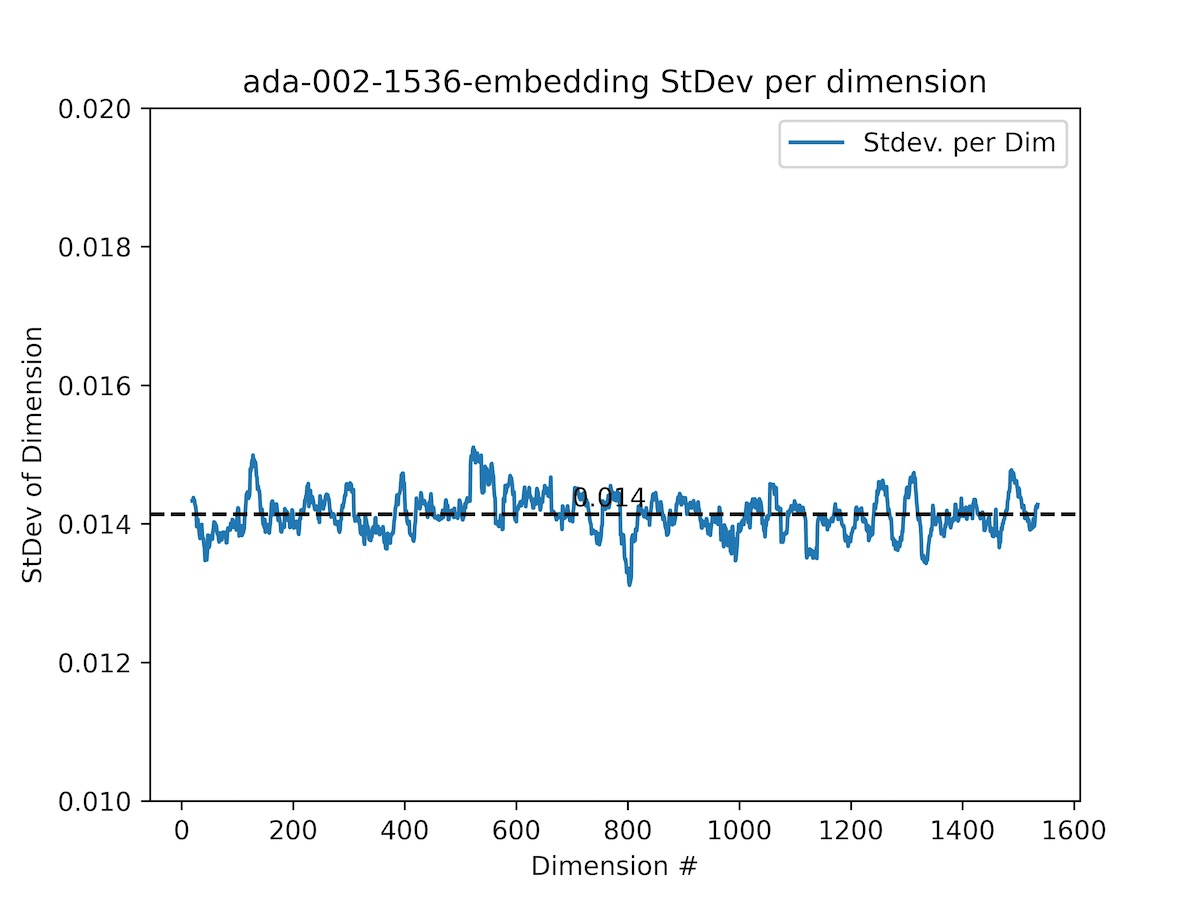 |
This graphs shows the smoothed standard deviation per dimension across 10k random samples from DBpedia embedded with the new text-emb3-large model and the old ada-002 model.
We can see the standard deviation is a multi-step function of the dimension index - earlier dimensions capture more information and those later on capture less. The graph also tells us that the OpenAI embedding model was trained with 4 aggregated loss functions at dimensions = {512d, 1024d, 1536d, 3072d} in the MRL style detailed above.
What's more interesting is that the information within the steps(512d, 1024d, 1536d, 3072d) diffuses more or less evenly amongst the dimensions. This also explains the magical finding in the MRL paper that shows you can actually take dimensions between these pre-specified chunks (eg. 750d) and still get incremental benefits.
Visualizing a Matryoshka Vector Space
Another interesting question we can ask is: How does the underlying data representation/vector-space change as you use more and more dimensions of a Matryoshka embedding?
In this video below every frame is a 3D vector space that was generated using principal components analysis(PCA) on upto only a certain number of MRL vector dimensions.
We took 10k random samples, embedded using the OpenAI text-embed-3-large model, from the same dataset linked above and then reduced them down to 3D space using PCA; we started off using only 4-dims all the way up to using all 3072-dims.
You can see that by the time we get to using 512 dims, the structure of the vector space is already well defined, after these inital 512 dimensions the others are mainly used to tighten data representation inside the larger structure.
By the time we get to dims 2000+ we only see small jittering of the data points, probably because the contributions of the incremental dimensions are negligible and can't be seen in the first 3 principal components.
Getting Familiar with OpenAI’s Matryoshka Embeddings
OpenAI has released two new models, text-embedding-3-small and text-embedding-3-large, which are trained using the Matryoshka Representation Learning technique. The API of these models supports a dimensions parameter with which you can control the length of the resulting embedding.
If you embed the same text with the same model but with a different dimensions parameter, you can see that the shorter embedding is not the truncated version of the longer one.
# !pip install openai
from openai import OpenAI
openai = OpenAI()
def vectorize(text,
dimensions,
model = "text-embedding-3-small"):
text = text.lower()
return openai.embeddings.create(input = [text],
model = model,
dimensions = dimensions).data[0].embedding
example_text = "Learned representations are a central component in modern ML systems, serving a multitude of downstream tasks."
full = vectorize(example_text, dimensions = 1536)
short = vectorize(example_text, dimensions = 8)
print(full[:8])
print(short)
[-0.001463836757466197, -0.0241670124232769, 0.00683123804628849, -0.013936602510511875, 0.0320618636906147, 0.00872271228581667, 0.031053075566887856, 0.021820487454533577]
[-0.025210261344909668, -0.41620534658432007, 0.11764788627624512, -0.24001678824424744, 0.5521708130836487, 0.15022294223308563, 0.5347974300384521, 0.3757933974266052]
However, if you examine their cosine similarity, you can see that they are very similar (or even equal due to rounding).
from sklearn.metrics.pairwise import cosine_similarity
cosine_similarity([full[:8]], [short])
array([[1.]])
If you take an even closer look, you can see that the embeddings actually only differ by a scaling factor (of 0.058 in this case).
scale = full[0]/short[0]
print(scale)
print([x * scale for x in short])
print(full[:8])
0.05806511632065122
[-0.001463836757466197, -0.0241670118626955, 0.006831238201508919, -0.01393660272831134, 0.03206186249057062, 0.008722712614794586, 0.031053074983168057, 0.021820487334108546]
[-0.001463836757466197, -0.0241670124232769, 0.00683123804628849, -0.013936602510511875, 0.0320618636906147, 0.00872271228581667, 0.031053075566887856, 0.021820487454533577]
Note that text-embedding-3-large and text-embedding-3-small differ in the length of the default embedding length:
- Default dimension for
text-embedding-3-small: 1536 - Default dimension for
text-embedding-3-large: 3072
Additionally, they do not produce compatible embeddings when sliced to the same size:
large = vectorize(example_text, dimensions = 3072, model = "text-embedding-3-large")
small = vectorize(example_text, dimensions = 1536, model = "text-embedding-3-small")
print(large[:1536])
print(small)
cosine_similarity([large[:1536]], [small])
[0.011070899665355682, 0.014488349668681622, -0.021118611097335815, -0.011152755469083786, 0.011555208824574947, -0.0007622754783369601, ... ]
[-0.001463836757466197, -0.0241670124232769, 0.00683123804628849, -0.013936602510511875, 0.0320618636906147, 0.00872271228581667, ... ]
array([[-0.00149749]])
Note that if you need to change the embedding dimension after you generate it, you need to normalize the embedding dimensions. The OpenAI documentation explains this more fully.
Example: How to Use Matryoshka Embeddings in Weaviate
This section quickly guides you through the steps to use OpenAI’s Matryoshka embeddings with the Weaviate vector database.
First you need to pip install the relevant Python packages.
pip install -U weaviate-client
Next, you need to setup a Weaviate vector database instance. For this example, you can start up a local instance of Weaviate via Docker, as follows:
docker run -p 8080:8080 -p 50051:50051 cr.weaviate.io/semitechnologies/weaviate:1.25.0
Once your vector database instance is up and running, you can connect to it as shown below:
import weaviate
client = weaviate.connect_to_local()
With default dimensions
As the OpenAI models are tightly integrated with Weaviate, you can use them through the text2vec_openai module, which enabled automatic vectorization of data at import and query time. You only need to define the model name and the dimensions. The text2vec_openai
module has some pre-defined dimensions. Available default dimensions for these models in Weaviate can be found in our documentation and are:
text-embedding-3-small: 512, 1536text-embedding-3-large: 256, 1024, 3072
from weaviate.classes.config import Property, DataType
# Define schema and create collection
my_collection = client.collections.create(
name="MyCollection",
vectorizer_config=wvc.config.Configure.Vectorizer.text2vec_openai(model='text-embedding-3-small',
dimensions = 512,
vectorize_collection_name=False,
),
properties=[
Property(name="text",
data_type=DataType.TEXT,
vectorize_property_name=False,
),
]
)
# Insert single data object
my_collection.data.insert({
"text": example_text,
})
With custom dimensions
If you want to use Matryoshka embeddings with a different value for the dimensions parameter, you will need to manually generate the embeddings at import and query time.
from openai import OpenAI
from weaviate.classes.config import Property, DataType
openai = OpenAI()
# Define function to embed text
def vectorize(text,
dimensions,
model = "text-embedding-3-small"):
text = text.lower()
return openai.embeddings.create(input = [text],
model = model,
dimensions = dimensions).data[0].embedding
# Define schema and create collection
my_collection = client.collections.create(
name="MyCollection",
properties=[
Property(name="text", data_type=DataType.TEXT),
]
)
# Insert single data object
my_collection.data.insert(
properties = {"text" : example_text},
vector = vectorize(example_text, dimensions=128),
)
Summary
This article introduced you to the Matryoshka Representation Learning technique, used to shorten embeddings, and showcased how you can use them in the Weaviate vector database.
You can learn more about Matryoshka embeddings in our Weaviate paper review on Matryoshka Representation Learning by Zain or in our 89th Weaviate podcast episode Matryoshka Embeddings with Aditya Kusupati, Zach Nussbaum, and Zain Hasan with Connor.
Ready to start building?
Check out the Quickstart tutorial, or build amazing apps with a free trial of Weaviate Cloud (WCD).
Don't want to miss another blog post?
Sign up for our bi-weekly newsletter to stay updated!
By submitting, I agree to the Terms of Service and Privacy Policy.
