
Why is this so incredibly fast?
Whenever I talk about vector search, I like to demonstrate it with an example of a semantic search. To add the wow factor, I like to run my queries on a Wikipedia dataset, which is populated with over 28 million paragraphs sourced from Wikipedia.
For example, I can query Weaviate for articles related to: "urban planning in Europe", and the vector database (in the case of my demo – Weaviate) responds with a series of articles about the topic, such as "The cities designed to be capitals".
You can try it for yourself by following this link, which is already pre-populated with the above question. Press the play button, to see the magic happen.
Here is the thing, finding the correct answer in a gigantic repository of unstructured data is not the most impressive part of this demonstration (I mean, it is very impressive), but it is the 🚀 speed at which it all happens. It takes a fraction of a second for the UI to show the results.
We are talking about a semantic search query, which takes milliseconds to find an answer in a dataset containing 28 million paragraphs. Interestingly enough, it takes longer to render the results than it takes the vector database to find the answer.
Note, a semantic search is unlike a regular keywords search (which matches keywords like-for-like), but instead, we are searching for answers based on the semantic meaning of our query and data.
The inevitable question that follows up this demonstration is always:
Why is this so incredibly fast?
What is a vector search?
To answer this question we need to look at how vector databases work.
Vector databases index data, unlike other databases, based on data vectors (or vector embeddings). Vector embeddings capture the meaning and context of data, usually predicted by Machine Learning models.
At the time of entry/import (or any significant changes to data objects), for every new/updated data object, vector databases use Machine Learning models to predict and calculate vector embeddings, which then are stored together with the object.
Every data object in a dataset gets a vector
In a nutshell, vector embeddings are an array of numbers, which can be used as coordinates in a high-dimensional space. Although it is hard to imagine coordinates in more than 3-dimensional space (x, y, z), we can still use the vectors to compute the distance between vectors, which can be used to indicate similarity between objects.
There are many different distance metrics, like cosine similarity and Euclidean distance (L2 distance).
The search part
In a similar fashion, whenever we run a query (like: "What is the tallest building in Berlin?"), a vector database can also convert it to a "query" vector. The task of a vector database is to identify and retrieve a list of vectors that are closest to the given vector of your query, using a distance metric and a search algorithm.
This is a bit like a game of boules – where the small marker (jack) is the location of our query vector, and the balls (boules) are our data vectors – and we need to find the boules that are nearest to the marker.
k-nearest neighbors (kNN)
One way to find similar vectors is with a simple k-nearest neighbors (kNN) algorithm, which returns the k nearest vectors, by comparing every data vector in the database to the query vector.
In our boules example (as illustraded below), with 6 boules, the kNN algorithm would measure the distance between the jack and each of the 6 boules on the ground. This would result in 6 separate calaculations.
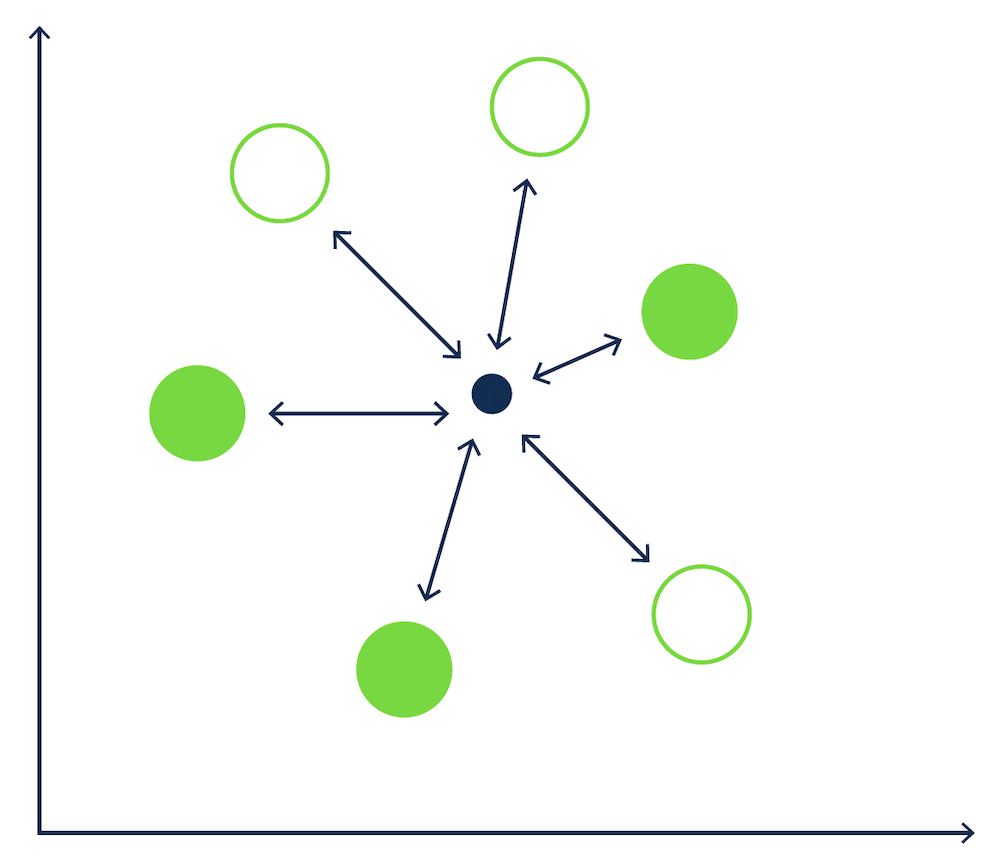
[Figure 1 - kNN search in a game of Boules.]
A kNN search is computationally very expensive
Comparing a search vector with 10, 100, or 1000 data vectors in just two dimensions is an easy job. But of course, in the real world, we are more likely to deal with millions (like in the Wikipedia dataset) or even billions of data items. In addition, the number of dimensions that most ML models use in semantic search goes up to hundreds or thousands of dimensions!
The brute force of a kNN search is computationally very expensive - and depending on the size of your database, a single query could take anything from several seconds to even hours (yikes😅). If you compare a vector with 300 dimensions with 10M vectors, the vector search would need to do 300 x 10M = 3B computations! The number of required calculations increases linearly with the number of data points (O(n)) (Figure 2).
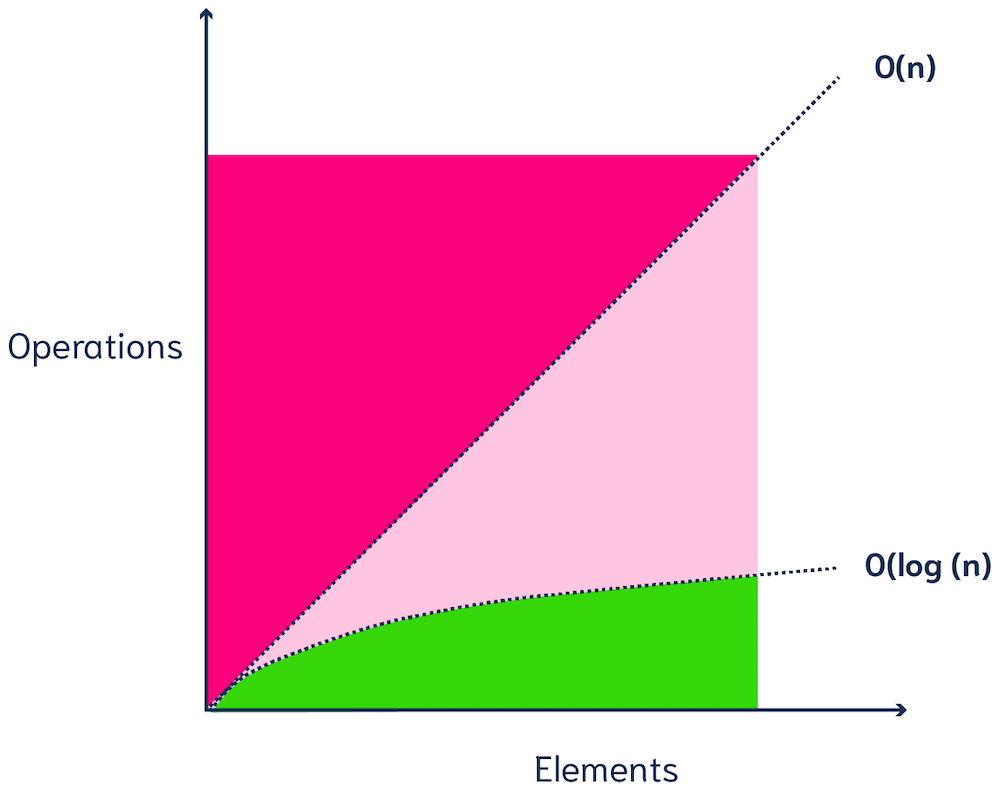
[Figure 2 - O(n) and O(log n) complexity]
In summary, kNN search doesn't scale well, and it is hard to image using it with a large dataset in production.
The answer - Approximate nearest neighbors (ANN)
Instead of comparing vectors one by one, vector databases use Approximate Nearest Neighbor (ANN) algorithms, which trade off a bit of accuracy (hence the A in the name) for a huge gain in speed.
ANN algorithms may not return the true k nearest vectors, but they are very efficient. ANN algorithms maintain good performance (sublinear time, e.g. (poly)logarithmic complexity, see Figure 2) on very large-scale datasets.
Note that most vector databases allow you to configure how your ANN algorithm should behave. This lets you find the right balance between the recall tradeoff (the fraction of results that are the true top-k nearest neighbors), latency, throughput (queries per second) and import time.
For a great example, check Weaviate benchmarks, to see how three parameters – efConstruction, maxConnections and ef - affect recall, latency, throughput and import times.
Examples of ANN algorithms
Examples of ANN methods are:
- trees – e.g. ANNOY (Figure 3),
- proximity graphs - e.g. HNSW (Figure 4),
- clustering - e.g. FAISS,
- hashing - e.g. LSH,
- vector compression - e.g. PQ or SCANN.
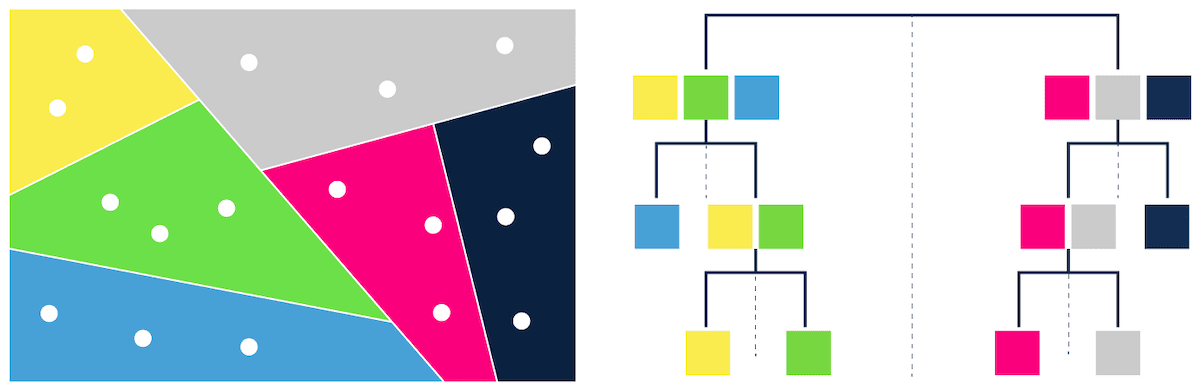
[Figure 3 - Tree-based ANN search]
Which algorithm works best depends on your project. Performance can be measured in terms of latency, throughput (queries per second), build time, and accuracy (recall). These four components often have a tradeoff, so it depends on the use case which method works best.
So, while ANN is not some magic method that will always find the true k nearest neighbors in a dataset, it can find a pretty good approximation of the true k neighbors. And it can do this in a fraction of the time!
HNSW in Weaviate
Weaviate is a great example of a vector database that uses ANN algorithms to offer ultra-fast queries. The first ANN algorithm introduced to Weaviate is a custom implementation of Hierarchical Navigable Small World graphs (HNSW).
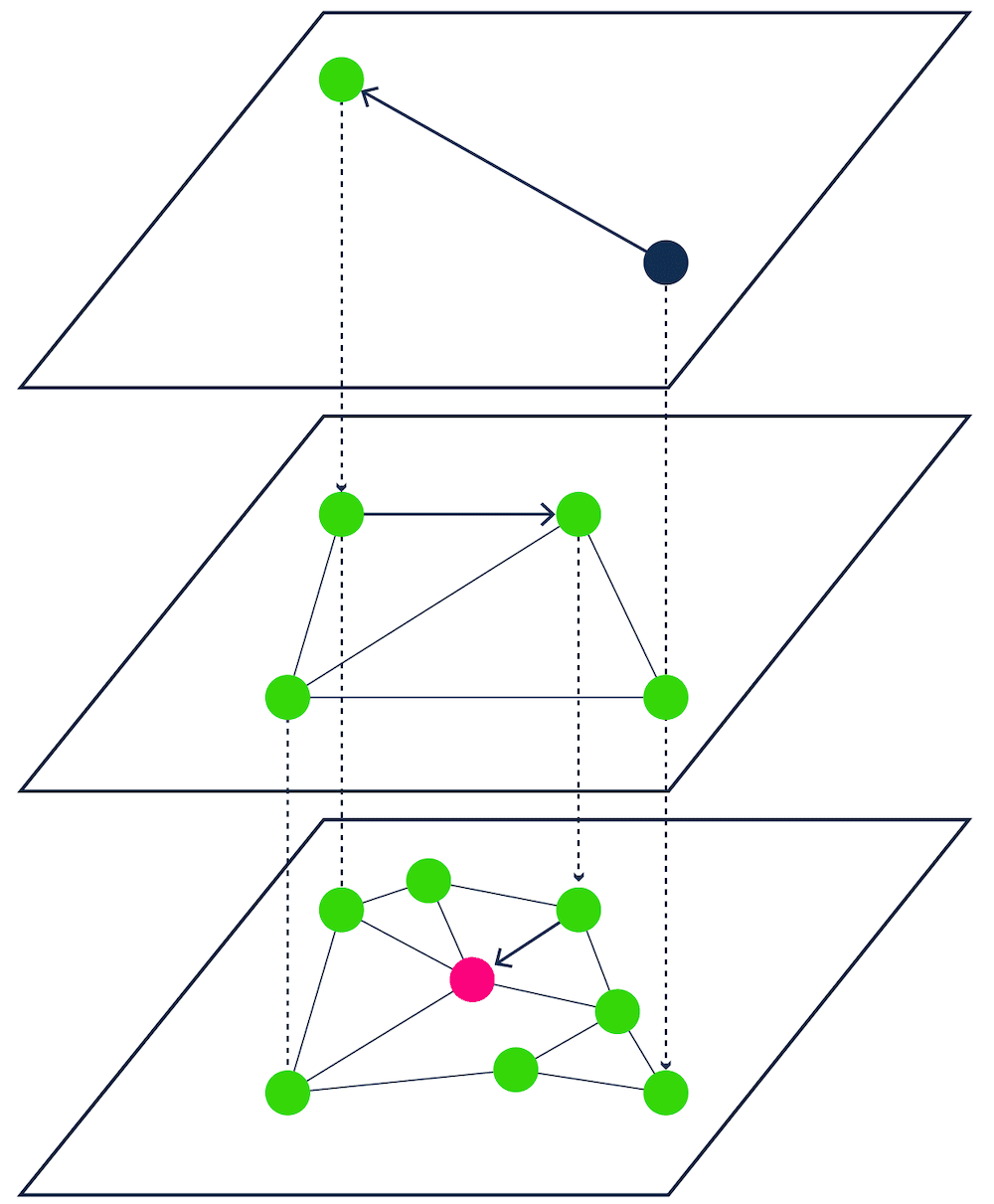
[Figure 4 - Proximity graph-based ANN search]
Check out Weaviate ANN benchmarks to see how HNSW performed on realistic large-scale datasets. You can use it to compare the tradeoffs between recall, QPS, latency, and import time.
You will find it interesting to see, that Weaviate can maintain very high recall rates (>95%), whilst keeping high throughput and low latency (both in milliseconds). That is exactly what you need for fast, but reliable vector search!
Summary
A quick recap:
- Vector databases use Machine Learning models to calculate and attach Vector embeddings to all data objects
- Vector embeddings capture the meaning and context of data
- Vector databases offer super fast queries thanks to ANN algorithms
- ANN algorithms trade a small amount of accuracy for huge gains in performance
Of course, there is a lot more going on in a vector database that makes it so efficient. But that is content for another article.😉
Learn more
The Weaviate Core team is currently working on research and implementation for other ANN algorithms. We are going to publish some of our findings in the next couple of weeks. So, stay tuned for more content on the topic.
Until then, you can listen to a podcast about ANN Benchmarks with Connor and Etienne from Weaviate.
Ready to start building?
Check out the Quickstart tutorial, or build amazing apps with a free trial of Weaviate Cloud (WCD).
Don't want to miss another blog post?
Sign up for our bi-weekly newsletter to stay updated!
By submitting, I agree to the Terms of Service and Privacy Policy.
