Embedding models
Embeddings are critical to vector databases such as Weaviate, as they enable vector/semantic search. Vector databases such as Weaviate allow users to store and search through millions, or even billions, of these embeddings with ease.
If generative models are the celebrities of the AI world, embedding models may be its plumbing; they’re not glamorous, but critical parts of the infrastructure.
Let's take a look at what embedding models are, and why they are so important.
How embedding models work
An embedding model seeks to capture a “meaning” of the input provided to it. The output embedding can then be used later for tasks such as classification, clustering, or most commonly, information retrieval.
Commonly used embedding models include Cohere’s embed-multilingual-v3.0, OpenAI’s text-embedding-3-large and Snowflake’s snowflake-arctic-embed-l-v2.0.
These names tend to be more generic and descriptive. Combined with their less glamorous status, these models may not be as well-known.
But they are no less interesting than generative models, and often share many similarities with them. For example, both of them take a text input and convert it to a numerical format with a tokenizer. One key difference is that where a generative model outputs a token at a time, an embedding model outputs a fixed length (or shape) of numbers.
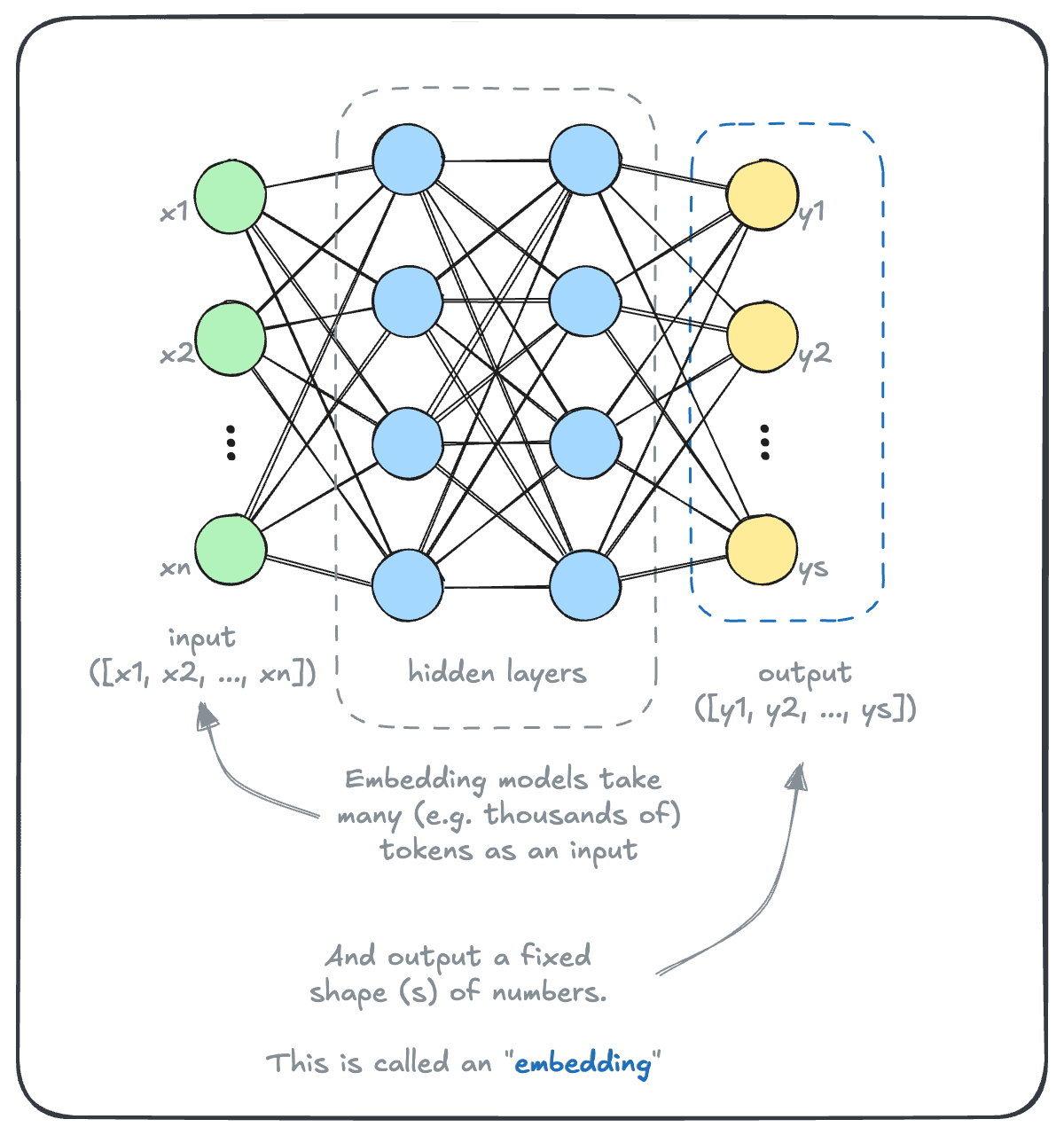
The concept of numerically representing a meaning may be foreign at first. Let's take a step back and look at a simpler example.
An analogy - color encoding
An analog for this approach can be found in how we represent colors as numbers - whether it be the RGB, CMYK or HSL system.
Each system can represent any color as a series of numbers. Take the official web color definition of “red” as an example. In RGB it is [255, 0, 0], in CMYK it is [0, 100, 100, 0], and in HSL it is [0, 100%, 50%].
In other words, each system is a standardized method of representing a color as a set of numbers.
Embedding models work similarly. For example, the phrase “You’re a wizard, Harry.”, may be represented as:
[0.021, -0.103, 0.036, 0.088, -0.022, ..., 0.056]
Where the actual sequence length may be quite large, such as 256, 1024, or 1536 values typically.
To be clear, modern embedding models are far more complex than algorithms that convert colors to RGB values. However, the principle is the same - each system consistently converts its inputs into a sequence of numbers.
How is this useful? As it turns out, for a variety of tasks.
Why use embedding models?
Earlier, we likened embedding models to numerical systems like RGB that can encode color. The key benefit of embedding models is similar to that of color encoding systems; they enable meaningful comparisons of the source object.
Going back to RGB colors, “crimson” is [220, 20, 60]. You can see that it is quite similar to red’s RGB value of [255, 0, 0], and very different to, say, the RGB value of “aqua”, which is [0, 255, 255].
| R | G | B | |
|---|---|---|---|
| Red | 255 | 0 | 0 |
| Crimson | 220 | 20 | 60 |
| Aqua | 0 | 255 | 255 |
In fact, we can quantify the similarity to a single number. We can use a commonly used metric called a “cosine” similarity. Here is an example implementation using Python:
import numpy as np
def cosine_similarity(a: list, b: list) -> float:
# Calculate the cosine similarity between two input lists
return np.dot(a, b) / (np.linalg.norm(a) * np.linalg.norm(b))
We can put the results of our comparison into a table, into what is called a similarity matrix. Here, each table cell value is the similarity between its corresponding row and the column.
| Red | Crimson | Aqua | |
|---|---|---|---|
| Red | 1 | 0.961 | 0 |
| Crimson | 0.961 | 1 | 0.247 |
| Aqua | 0 | 0.247 | 1 |
The key takeaway from this demonstration is that the system allows us to compare how similar each color is. Conversely, we now have a way in which we can identify the most similar color to a given color in a bag of colors.
Applications of embedding models
Going back to our embedding models, the value of embedding models is that it allows us to identify the object with the most similar meaning to a given object, in a set of objects.
Take these three pieces of text:
1. "You're not wizened, Harry."
2. "Harry can wield magic."
3. "Ron is not a great driver."
Which one might be most similar to "You're a wizard, Harry."?
Most of us would probably answer 2. But why? And how would you get a program to answer in the same way? Note that 2 only includes one overlapping word with the query.
That’s the task that embeddings enable. Using embeddings and cosine similarity, we see that:
| Rank | Cosine distance | |
|---|---|---|
| Harry can wield magic. | 1 | 0.238 |
| You're not wizened, Harry. | 2 | 0.274 |
| Ron is not a great driver. | 3 | 0.803 |
This concept of similarity is used in semantic search. In modern AI systems, semantic search is a critical component of retrieval augmented generation (RAG), helping to complement generative systems by providing it with accurate, up-to-date context to work with.
Applications of embeddings go even further. Embeddings are used in other AI systems such as recommenders, clustering and classification and so on.
In this section, we largely talked about aspects related to text embedding models, where a text input is used to generate a vector embedding.
Just like generative models, the world of embedding models is very big and interesting. Multi-modal embedding models can take various input types and produce compatible embeddings in the same space. And modern embeddings may come in different formats, using techniques such as multi-vector embeddings (e.g. ColBERT) or adaptive-length embeddings.
We may touch on them later on, when we get to further in-depth discussions about specific modalities or model selection.
Questions and feedback
If you have any questions or feedback, let us know in the user forum.
